The explanation, if we want to call it that, for the wider mass distribution for shorter-lived partices lies close to the heart of quantum mechanics, in the energy-time version of Heisenberg's uncertainty principle. That principle is represented by the equation,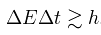
where the width of the energy distribution, delta E, times the length of time during which the particle might decay, delta t, must be no less than a constant value, known as Plank's constant, h. Shorter-lived particles have very small delta t and thus must have larger delta E, or a wider energy distribution–in our case, a wider dilepton mass distribution–in order to satisfy this inequality. Why this inequality should hold is another matter, taking us to interpretations of quantum mechanics. But that it does hold is a fundamental property of nature.

So more massive particles are shorter-lived, and shorter-lived particles have greater uncertainty in their mass distribution. This (together with measurement uncertainty that increases with energy) is a second reason why distributions along the dimuon mass spectrum are wide. Because these distributions are wide and overlapping, no single cause can be attributed to any particular event; there are always multiple physical processes that might have produced an event of that type. And thus particle identification is based on statistical analysis of many different events, plotted in histograms.

Wikipedia explanation of the Heisenberg Principal